Мастер-класс по решению задач «Части В» ЕГЭ по математике
Посмотреть бесплатный онлайн-разбор варианта
1. В летнем лагере 164 ребенка и 23 воспитателя. Автобус рассчитан не более чем на 45 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
1. Бегун пробежал 400 метров за 45 секунд. Найдите среднюю скорость бегуна. Ответ выразите в километрах в час.
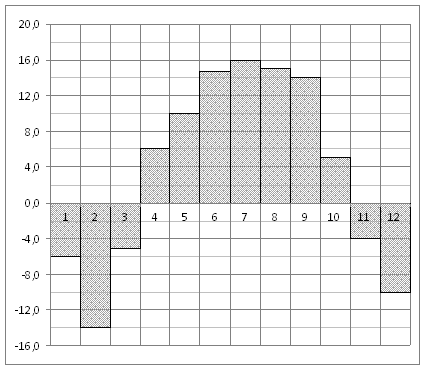
2. На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали -- температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с положительной среднемесячной температурой.
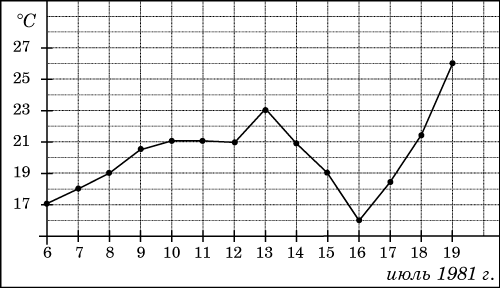
2. На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали -- температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какая была температура 15 июля. Ответ дайте в градусах Цельсия.
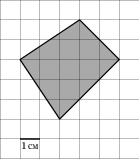
3. На клетчатой бумаге с размером клетки $1 \textrm{ см}\times 1 \textrm{ см}$ изображен четырехугольник. Найдите его площадь. Ответ дайте в квадратных сантиметрах.
3. Найдите длину диагонали прямоугольника, вершины которого имеют координаты $\left(2;1\right)$, $\left(2;4\right)$, $\left(6;1\right)$, $\left(6;4\right)$.
4. За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
4. В Волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня. Сегодня 28 марта, погода в Волшебной стране хорошая. Найдите вероятность того, что 1 апреля в Волшебной стране будет отличная погода.
5. Найдите корень уравнения $7^{6x-5} = 7$.
5. Найдите корень уравнения $\log_{2}\left(4-x\right)=7$.
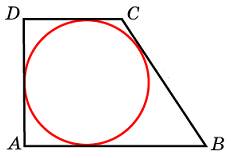
6. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
6. У треугольника со сторонами 12 и 15 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 10. Найдите длину высоты, проведенной ко второй стороне.
7. На рисунке изображен график функции $y=F(x)$ -- одной из первообразных функции $f(x)$, определенной на интервале $(-3;5)$. Найдите количество решений уравнения $f(x)=0$ на отрезке $[-2;4]$.

7. На рисунке изображен график $y = f'(x)$ -- производной функции $f(x)$ и шесть точек на оси абсцисс: $x_1$, $x_2$, \ldots, $x_6$. В скольких из этих точек функция $f(x)$ возрастает?

8. Объем треугольной пирамиды равен 94. Через вершину пирамиды и среднюю линию ее основания проведена плоскость. Найдите объем отсеченной треугольной пирамиды.
8. Шар вписан в цилиндр объемом 42. Найдите объем шара.
9. Найдите значение выражения $\dfrac{5\sin74^{\circ}}{\cos37^{\circ}\cdot \cos53^{\circ}}$.
9. Найдите значение выражения $(432^2-568^2):1000$.
10. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: $T(t) = T_0 + bt + at^2$, где $t$ -- время (в мин), $T_0 = 680$ К, $a = -16$ К/мин$^2$, $b = 224$ К/мин. Известно, что при температуре нагревательного элемента свыше 1400 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.
10. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением $a$ км/ч$^2$ . Скорость вычисляется по формуле $v= \sqrt{2\ell a}$, где $\ell$ -- пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 1,1 километра, приобрести скорость 110 км/ч. Ответ выразите в км/ч$^2$.
11. Имеется два сплава. Имеется два сплава. Первый сплав содержит 5% меди, второй -- 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
11. Первая труба заполняет бассейн за 7 часов, а две трубы вместе -- за 5 часов 50 минут. За сколько часов заполняет бассейн одна вторая труба?
12. Найдите точку минимума функции $y = 1,5 x^2 - 27x + 42 \ln x - 10$.
12. Найдите наибольшее значение функции $y=4\cos x-20x+7$ на отрезке $\left[0;\dfrac{3\pi}{2}\right]$.







